Question

Researchers suspect that 18% of all high school students smoke at least one pack of cigarettes a day. At the local high school, a randomly selected sample of 300 students found that 50 students smoked at least one pack of cigerattes a day. At a = 0.025, test the claim that less than 18% of all high school students smoke at least one pack of cigarettes a day.

What is the appropriate test?

a. z-test for proportions

b. t-test for the mean

c. z-test for the mean

d. chi - square for variance

Why?

If the test value is z = -0.601 and P = 0.2743, what is the conclusion (is it supported)?

Answer 1

We conclude that 18% of all high school students smoke at least one pack of cigarettes a day.

Explanation:

We are given that researchers suspect that 18% of all high school students smoke at least one pack of cigarettes a day.

At the local high school, a randomly selected sample of 300 students found that 50 students smoked at least one pack of cigarettes a day.

Let p = proportion of all high school students who smoke at least one pack of cigarettes a day.

So, Null Hypothesis,
`H_0` : p = 18% {means that 18% of all high school students smoke at least one pack of cigarettes a day}

Alternate Hypothesis,
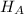`H_A` : p < 18% {means that less than 18% of all high school students smoke at least one pack of cigarettes a day}

The test statistics that would be used here is One-sample z -test for proportions because we are given with the proportions values;

T.S. =
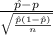`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
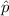`\hat p` = sample proportion of students who smoked at least one pack of cigarettes a day =
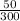`(50)/(300)` = 0.167

n = sample of students = 300

So, test statistics =
`\frac{0.167-0.18}{\sqrt{(0.167(1-0.167))/(300) } }`

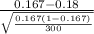
= -0.604

The value of z test statistics is -0.604.

Also, P-value of the test statistics is given to us is 0.2743.

Since, the P-value of test statistics is more than the level of significance as 0.2743 > 0.025, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that 18% of all high school students smoke at least one pack of cigarettes a day.