Question

When estimating yˆ = β0 + β1x1 + β2x2 + ε, the following regression results using ANOVA were obtained.

df SS MS F
Regression 2 210.9 105.5 114.7
Residual 17 15.6 0.92
Total 19 226.5
Coefficients Standard Error t-stat p-value
Intercept −1.6 0.57 −2.77 0.0132
x1 −0.5 0.04 −15.11 2.77E-11
x2 0.1 0.07 1.89 0.0753

Which of the following is the adjusted R2?

A. 0.92
B. 0.82
C. 0.96
D. 0.86

Answer 1

A) The adjusted R² = 0.923

Explanation:

Given data

sum of squares of regression (SSR) = 210.9

Sum of squares of residuals = 15.6

Total sum of squares(SST) = 226.5

Degrees of freedom of Regression = 2

Degrees of freedom of Residuals = 17

Total number of degrees of freedom = 19

The R² is determined by

`R^(2) = (Regression SS)/(Total SS)`

`R^(2) = (210.9)/(226.5) = 0.9311`

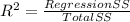
Adjusted R² is determined by

R⁻²
`= 1-(1-R^(2))((n-1)/(n-k-1)))`

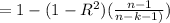
The degrees of freedom of residuals

n -k-1 = 17

given data k= 2 (degrees of freedom of regression = 2)

n - 2 -1 =17

n = 17 +3 =20

The Adjusted R²

`= 1-(1-R^(2))((n-1)/(n-k-1)))`

`= 1-(1-0.9311)((20-1)/(17))`

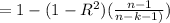
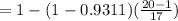
on calculation, we get

R⁻² = 0.923

Final answer:-

The adjusted R² = 0.923