Question

Miles invested $2400 into a retirement account that earns 1.8% interest compounded bimonthly. Write a function to model this situation, then

find the balance of the account after 25 years.

Answer 1

(a)
`A(n)=P(1+(r)/(24))^(24n)`

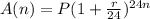
(b)$3763.31

Explanation:

When a Principal, P is invested at an annual rate r, for a period of k times over n years, the Amount, A(t) after n years is given by the model:

`A(n)=P(1+(r)/(k))^(nk)`

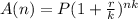
In this case:

r=1.8%

Since it is compounded bimonthly, k=2X12=24

Therefore:

`A(n)=P(1+(r)/(24))^(24n)`

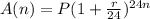
For P=$2400, and n=25 years

`A(25)=2400(1+(0.018)/(24))^(24*25)\\A(25)=\$3763.31`

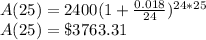
The balance in the account after 25 years is $3763.31.