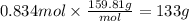Question

How many grams of Br2 are needed to completely convert 15.0 g Al to AlBr3 ?

Al (s) + Br2 (l) --> AlBr3 (hint: the equation is not balanced)

Answer 1

133 g

Step-by-step explanation:

Step 1: Write the balanced equation

2 Al(s) + 3 Br₂(l) ⇒ 2 AlBr₃(s)

Step 2: Calculate the moles corresponding to 15.0 g of Al

The molar mass of aluminum is 26.98 g/mol. The moles corresponding to 15.0 g of Al are:

`15.0g * (1mol)/(26.98g) = 0.556mol`

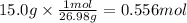
Step 3: Calculate the moles of Br₂ that react with 0.556 moles of Al

The molar ratio of Al to Br₂ is 2:3. The moles of bromine that react with 0.556 moles of aluminum are:

`0.556molAl * (3molBr_2)/(2molAl) = 0.834molBr_2`

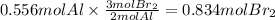
Step 4: Calculate the mass corresponding to 0.834 moles of Br₂

The molar mass of bromine is 159.81 g/mol. The mass corresponding to 0.834 moles of Br₂ is:

`0.834mol * (159.81g)/(mol) = 133 g`