Question

Please help!! 16!/2!14!

Answer 1

1

Explanation:

16!/16!=1

Answer 2

Answer: 120

========================================================

Work Shown:

The exclamation mark indicates we start at the given number and multiply our way down to 1.

16! = 16*15*14*13*12*11*...*3*2*1

14! = 14*13*12*11*...*3*2*1

2! = 2*1

Note how 14*13*12*11*...*3*2*1 is buried in the sequence for 16! and it is entirely 14! expression.

This means we can say

16! = 16*15*14*13*12*11*...*3*2*1

16! = 16*15*14!

Bold terms to show the replacement being done.

This will allow us to cancel

`(16!)/(2!*14!) = (16*15*14!)/(2!*14!) = (16*15)/(2!) = (16*15)/(2*1)`

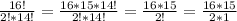
The 14! expressions divide and cancel out.

Then we simplify completely

`(16*15)/(2*1) = (240)/(2) = 120`

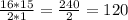
Therefore,

`(16!)/(2!*14!) = 120`

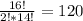
Side note: This expression is the result of computing
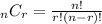`_nC_r = (n!)/(r!(n-r)!)` for n = 16 and r = 2. This is the combination formula. This is equivalent to n = 16 and r = 14 due to symmetry.