Question

Elizabeth Kennedy sells beauty supplies. Her annual demand for a particular skin sparkle is 17,000 units. The cost of placing an order is $50, while the holding cost per unit per year is 20 percent of the cost. This item currently costs $12.50 if the order quantity is less than 1500. For orders of 1501 units up to 10,000 units the cost falls to $12.45 and for orders of 10,001 or greater, the cost falls to $12.40. To minimize total cost, Elizabeth must order the right number of units. What is the value of this minimum cost

Answer 1

The minimum cost will be "$214085".

Step-by-step explanation:

`D = 1700 units \\\\S = \$ 50 \\\\H= 20%\\`

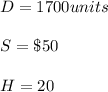
i) When quantity = 1-1500, price = $ 12.50 , and holding price is $12.50 * 20 %= $2.50.

ii) When quantity = 1501 -10,000, price = $ 12.45 , and holding price is $12.45 * 20 %= $2.49.

iii) When quantity = 10,0001- and more, price = $ 12.40 , and holding price is $12.40 * 20 %= $2.48.

`EOQ= \sqrt{(2DS)/(H)} \\\\EOQ1= \sqrt{(2* 17000* 50)/(2.50)} \\\\EOQ1=824.62 \ \ \ or \ \ \ 825\\`

`EOQ2= \sqrt{(2* 17000* 50)/(2.49)} \\\\EOQ1=826.2T \ \ \ or \ \ \ 826\\`

`EOQ3= \sqrt{(2* 17000* 50)/(2.48)} \\\\EOQ3=827.93 \ \ \ or \ \ \ 828\\`

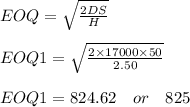
know we should calculate the total cost of EOQ1 and break ever points (1501 to 10,000)units

`total \ cost = odering \ cost + holding \ cost + \ Annual \ product \ cost\\\\total_c = (D)/(Q) * S + (Q)/(2) * H + (p * D) \\\\T_c = (17000)/(825) * 50+ (825)/(2) * 2.50 + (12.50 * 17000)\\\\T_c = 1030 .30 +1031.25+212500\\\\T_c =$ 214561.55\\\\`

`T_c = (17000)/(1501) * 50+ (1501)/(2) * 2.49 + (12.45 * 17000)\\\\T_c = 566.28 +1868.74+211650\\\\T_c =$ 214085.02 \ \ \ or \ \ \ $ 214085\\\\`

`T_c = (17000)/(10001) * 50+ (10001)/(2) * 2.48 + (12.40 * 17000)\\\\T_c = 84.99+ 12401.24+210800\\\\T_c =$ 223286.23 \\`

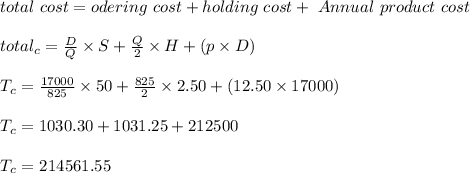
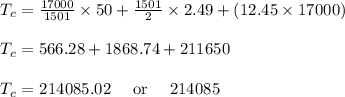
The total cost is less then 15001. So, optimal order quantity is 1501, that's why cost is = $214085.