Answer:
a) X=77 drivers
b) Power of the test = 0.404
c) Increasing the sample size.
Explanation:
This is a hypothesis test of proportions. As the claim is that the speed monitors were effective in reducing the speeding, this is a left-tail test.
For a left-tail test at a 5% significance level, we have a critical value of z that is zc=-1.645. This value is the limit of the rejection region. That means that if the test statistic z is smaller than zc=-1.645, the null hypothesis is rejected.
The proportion that would have a test statistic equal to this critical value can be expressed as:
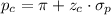
The standard error of the proportion is:
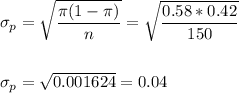
Then, the proportion is:
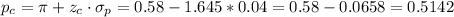
This proportion, with a sample size of n=150, correspond to
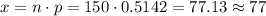
The power of the test is the probability of correctly rejecting the null hypothesis.
The true proportion is 0.52, but we don't know at the time of the test, so the critical value to make a decision about rejecting the null hypothesis is still zc=-1.645 corresponding to a critical proportion of 0.51.
Then, we can say that the probability of rejecting the null hypothesis is still the probability of getting a sample of size n=150 with a proportion of 0.51 or smaller, but within a population with a proportion of 0.52.
The standard error has to be re-calculated for the new true proportion:
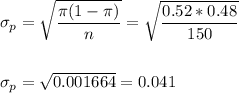
Then, we calculate the z-value for this proportion with the true proportion:
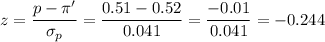
The probability of getting a sample of size n=150 with a proportion of 0.51 or lower is:
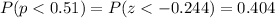
Then, the power of the test is β=0.404.
The only variable left to change in the test in order to increase the power of the test is the sample size, as the significance level can not be changed (it is related to the probability of a Type I error).
It the sample size is increased, the standard error of the proprotion decreases. As the standard error tends to zero, the critical proportion tend to 0.58, as we can see in its equation:
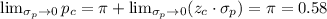
Then, if the critical proportion increases, the z-score increases, and also the probability of rejecting the null hypothesis.