Answer:
the optimal order size Q is 18.56 cars
the annual inventory cost = $12066.48
the order cycle time is 42.34 days
Step-by-step explanation:
Using the following expression to determine the optimal order size Q:
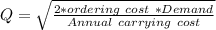
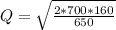
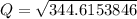
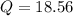
Hence; the optimal order size Q is 18.56 cars
The annual inventory cost is mathematically expressed as:
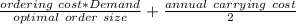
=
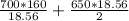
= 6034.482759 + 6032
= $12066.48276
≅ $12066.48
Hence, the annual inventory cost = $12066.48
For The order cycle time; we have;
Order cycle time =
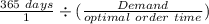
=
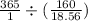
=
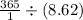
=
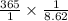
= 42.34 days
Hence, the order cycle time is 42.34 days