Question

According to a survey 60% of people have a dog. If 5 people are selected randomly, what is the probability that at least 2 of them have a dog ? Round your answer to the nearest tenth of a percent .

Answer 1

Probability that at least 2 of them have a dog is 0.913.

Explanation:

We are given that according to a survey 60% of people have a dog.

Also, 5 people are selected randomly.

The above situation can be represented through binomial distribution;

`P(X=r)=\binom{n}{r} * p^(r)* (1-p)^(n-r); x = 0,1,2,3,.....`

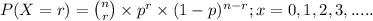
where, n = number of trials (samples) taken = 5 people

r = number of success

p = probability of success which in our question is probability

that people have a dog, i.e; p = 60%

Let X = Number of people who have a dog

SO, X ~ Binom(n = 5, p = 0.60)

Now, probability that at least 2 of them have a dog is given by = P(X
`\geq` 2)

P(X
`\geq` 2) = 1 - P(X < 2)

= 1 - P(X = 0) - P(X = 1)

=
`1-\binom{5}{0} * 0.60^(0)* (1-0.60)^(5-0)-\binom{5}{1} * 0.60^(1)* (1-0.60)^(5-1)`

=
`1-(1 * 1* 0.40^(5))-(5* 0.60^(1)* 0.40^(4))`

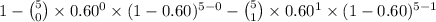
= 1 - 0.01024 - 0.0768

= 0.913

Therefore, probability that at least 2 of them have a dog is 0.913.