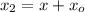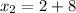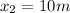Question

Part A At t tt = 2.0 s s , what is the particle's position? Express your answer to two significant figures and include the appropriate units. x x = nothing nothing SubmitRequest Answer Part B At t tt = 2.0 s s , what is the particle's velocity? Express your answer to two significant figures and include the appropriate units. v x vx = nothing nothing SubmitRequest Answer Part C At t tt = 2.0 s s , what is the particle's acceleration? Express your answer to two significant figures and include the appropriate units. a x ax = nothing nothing

Answer 1

The particle's position at t = 2.0 s cannot be determined without the specific displacement equation. Its velocity at t = 2.0 s is 2.125 m/s, and its acceleration is -0.0625 m/s².

Step-by-step explanation:

To find the particle's position, velocity, and acceleration at t = 2.0 s, we need to use the given equations and initial conditions. For Part A, without the specific displacement equation, we cannot determine the particle's position. For Part B, the velocity function is given by v(t) = A + Bt¯¹. Substituting the given values, A = 2 m/s and B = 0.25 m, into the equation gives us v(2.0) = 2 + 0.25/2 = 2.125 m/s. For Part C, to find the acceleration, we take the derivative of the velocity equation with respect to time, which yields a(t) = -Bt¯². Evaluating at t = 2.0 s, we get a(2.0) = -0.25 / (2.0)² = -0.0625 m/s².

Answer 2

Complete Question

The complete question is shown on the first uploaded image

Answer:

The particle's position is
`x_(2) = 10 m`

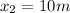
The particle's velocity is
`v = 2 \ m/s`

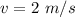
Step-by-step explanation:

From the question we are told that

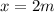`x = 2m` at
`t_o = 0 \ sec`

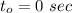
and from the graph at t = 0
`v = 6 /m`

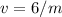
Now the acceleration which is the slope of the graph is mathematically represented as

`a = - (6 - 4)/(3-2)`

`a = - 2 m/s^2`

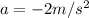
The negative sign shows that it is a negative slope

Now to obtain the velocity at t = 2 sec

We use the equation of motion as follows

`v = v_o + at`

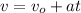
substituting values '

`v = 6 + (-2)(2)`

`v = 2 \ m/s`

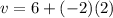
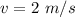
Now to obtain the position of the particle at v = 2 m/s

We use the equation of motion as follows

`v^2 = v_o ^2 + 2 ax`

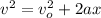
So
`2 ^2 = 6^2 + 2(-2)x`

`4x = 32`

`x = 8 m`

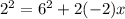
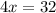
From above
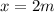`x = 2m` at
`t_o = 0 \ sec`

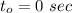
So the position at t = 2 s

`x_(2) = x + x_o`

`x_(2) = 2 + 8`

`x_(2) = 10 m`