Question

The demand function for jumbo packages of toilet paper is given by q=D(p)=0.25(270−p2) where q (measured in units of a hundred) is the quantity demanded per week and p is the unit price in dollars. (a) Find the elasticity function E(p)= equation editorEquation Editor (b) Evaluate the elasticity at 10. E(10)= equation editorEquation Editor (Keep at least 5 digits.) (c) Should the unit price be lowered slightly from 10 dollars in order to increase revenue? (d) Use the elasticity of demand to find the price which maximizes revenue for this product. p= equation editorEquation Editor dollars Round your answer to two decimal places as needed.

Answer 1

the solution is in the explanation

Step-by-step explanation:

q = D(p) = 0.25(250 -
`p^(2)`)

`d_(q)`/
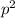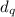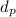`d_(p)` = 0.25 (0-2p) = -0.5p

a. Elasticity E(p) =
`\left[\begin{array}{ccc}p/q\\:\\d_(q)/d_(p) \end{array}\right]`

E(p) =
`\left[\begin{array}{ccc}p/0.25(270-p^(2)) X (-0.5)P \end{array}\right]`

E(P) = 2
`P^(2)`/270-
`P^(2)`

b. E(10) =2(100)/ 270 - 100 = 200/170 = 1.18

c. E(10) > 1

so the demand is elastic

hence unit price be lowered to increase revenue

yes

d. for maximum revenue: E(p) = 1

2
`P^(2)`/270-
`P^(2)` = 1

cross multiply you have 3
`P^(2)` = 270

P =
`(270/3)^(1/2)`

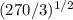
P = 9.48 dollars