Answer:
the final angular velocity = 1.942 rad/s²
Step-by-step explanation:
Let assume that the diameter is 1.0 m since we are not given the diagram.
So the force applied on one door is 65 N at 11° and at a distance of 1.0 m
Mass of each panel plate is 55 kg
Moment of inertia of the door about the center point O is:
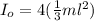
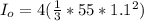
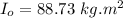
Using the conservation of angular momentum ; we have:
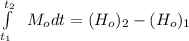
Then the moment of force about center point O is:
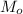 = (65 cos 11° )(1.0)
= (65 cos 11° )(1.0)
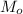 = 63.81 N-m
= 63.81 N-m
as moment is constant , it does not vary with time ; as much:
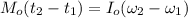
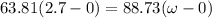
172.287 = 88.73 ω
ω = 172.287/88.73
ω = 1.942 rad/s²
Hence, the final angular velocity = 1.942 rad/s²