Question

Choose the correct answer below. A. Increasing the level of confidence has no effect on the interval. B. Increasing the level of confidence widens the interval. C. Increasing the level of confidence narrows the interval. D. It is not possible to tell the effect of increasing the level of confidence on the width of the interval since the requirements for constructing a confidence interval in parts​ (b) and​ (c) were not met. Click to select your answer(s).

Answer 1

`ME = t_(\alpha/2) (s)/(√(n))`

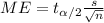
And the width for the confidence interval is given by:

`Width =2ME=2t_(\alpha/2) (s)/(√(n))`

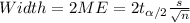
And we want to see the effect if we increase the confidence level for a interval. On this case if we increase the confidence level then the critical value for the confidence interval
`t_(\alpha/2)` would be higher and then the width of the interval would increase. So then the best answer for this case would be:

B. Increasing the level of confidence widens the interval.

Explanation:

Let's assume that we have a parameter of interest
`\mu` who represent for example the true mean for a population. And we can construct a confidence interval in order to estimate this parameter if we know the distribution for the statistic let's say
`\bar X` and for this particular example the confidence interval is given by:

`\bar X \pm ME`

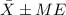
Where ME represent the margin of error for the estimation and this margin of error is given by:

`ME = t_(\alpha/2) (s)/(√(n))`

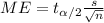
And the width for the confidence interval is given by:

`Width =2ME=2t_(\alpha/2) (s)/(√(n))`

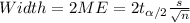
And we want to see the effect if we increase the confidence level for a interval. On this case if we increase the confidence level then the critical value for the confidence interval
`t_(\alpha/2)` would be higher and then the width of the interval would increase. So then the best answer for this case would be:

B. Increasing the level of confidence widens the interval.