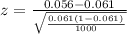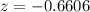Answer:
The value of the test statistic
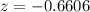
Explanation:
From the question we are told that
The high dropout rate is
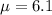 %
%
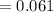
The sample size is
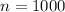
The number of dropouts
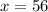
The probability of having a dropout in 1000 people
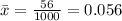
Now setting up Test Hypothesis
Null
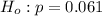
Alternative
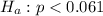
The Test statistics is mathematically represented as
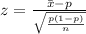
substituting values