Question

A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 415 gram setting. It is believed that the machine is underfilling the bags. A 44 bag sample had a mean of 410 grams. Assume the population variance is known to be 729. Is there sufficient evidence at the 0.05 level that the bags are underfilled?

Answer 1

There is not enough evidence to conclude that the bags of potato chips are underfilled.

Explanation:

In this case we need to determine whether the bag filling machine works correctly at the 415 gram setting.

The hypothesis can be defined as follows:

H₀: The bags of potato chips are not underfilled, i.e. μ = 415.

Hₐ: The bags of potato chips are underfilled, i.e. μ < 634.

The information provided is:

`n=44\\\bar x=410\\\sigma=√(729)=27\\\alpha=0.05`

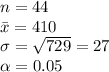
As the sample size is quite large, i.e. n = 44 > 30 and is taken form an unknown population, according to the Central limit theorem the sampling distribution of sample mean will follow the Normal distribution.

So, a z-test for single mean will be applied to perform the test.

Compute the test statistic value as follows:

`z=(\bar x-\mu)/(SD/√(n))\\\\=(410-415)/(27/√(44))\\\\=-1.23`

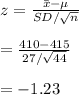
The test statistic value is -1.23.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected.

Compute the p-value for the one-tailed test as follows:

`p-value=P(Z <-1.23)\\=0.10935`

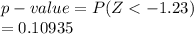
*Use a z-table for the probability.

The p-value of the test is 0.10935.

p-value = 0.10935 > 0.05

The null hypothesis will not be rejected.

Thus, there is not enough evidence to conclude that the bags of potato chips are underfilled.