Question

15. A researcher claims that the variation in the number of years of teaching experience of senior high school teachers is greater than the variation in the number of years of teaching experience of elementary teachers. Two groups are randomly selected. The variance of the number of years teaching of 18 elementary school teachers is 1.9 years and the variance of the number of years teaching of 15 high school teachers is 2.8 years. Compute the test statistic AND determine the critical value, using a 0.05 level of significance.

Answer 1

The value of F test statistics is 1.474 and the critical value using a 0.05 level of significance is 2.349.

Explanation:

We are given that two groups are randomly selected. The variance of the number of years teaching of 18 elementary school teachers is 1.9 years and the variance of the number of years teaching of 15 high school teachers is 2.8 years.

Let
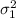`\sigma^(2) _1` = population variation in the number of years of teaching experience of senior high school teachers

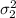`\sigma^(2) _2` = population variation in the number of years of teaching experience of senior elementary teachers

So, Null Hypothesis,
`H_0` :
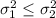`\sigma_1^(2) \leq \sigma_2^(2)` {means that the variation in the number of years of teaching experience of senior high school teachers is smaller or equal to the variation in the number of years of teaching experience of elementary teachers}

Alternate Hypothesis,
`H_A` :
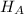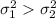`\sigma_1^(2) > \sigma_2^(2)` {means that the variation in the number of years of teaching experience of senior high school teachers is greater than the variation in the number of years of teaching experience of elementary teachers}

The test statistics that would be used here is Two-sample F test statistics;

T.S. =
`(s_1^(2) )/(s_2^(2) ) * (\sigma_2^(2) )/(\sigma_1^(2) )` ~
`F_n__1-1,n_2-1`

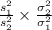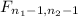
where,
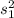`s_1^(2)` = sample variance number of years teaching of 15 high school teachers = 2.8 years

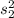`s_2^(2)` = sample variance number of years teaching of 15 elementary school teachers = 1.9 years

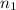`n_1` = sample of high school teachers = 15

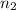`n_2` = sample of elementary school teachers = 18

So, the test statistics =
`(2.8 )/(1.9) * 1` ~
`F_1_4_,_1_7`

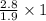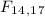
= 1.474

Hence, the value of F test statistics is 1.474.

Also, at 0.05 level of significance the F table gives critical value of 2.349 for right-tailed test at
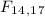`F_1_4_,_1_7` degree of freedom.