Question

The curves y = √x and y=(2-x) and the Cartesian axes form two distinct regions in the first quadrant. Find the volumes of rotation for each of the regions if rotating each around the horizontal axis and around the vertical axis. Construct the integral that represents the sum of the volumes of revolutions around the y-axis. Confirm that you get the same answer as when you revolve just the outer curve y=(2-x)'

Answer 1

Explanation:

If you graph there would be two different regions. The first one would be

`y = √(x) \,\,\,\,, 0\leq x \leq 1 \\`

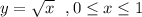
And the second one would be

`y = 2-x \,\,\,\,\,, 1 \leq x \leq 2`.

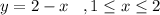If you rotate the first region around the "y" axis you get that

`{\displaystyle A_1 = 2\pi \int\limits_(0)^(1) x√(x) dx = (4\pi)/(5) = 2.51 }`

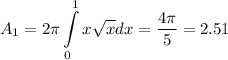
And if you rotate the second region around the "y" axis you get that

`{\displaystyle A_2 = 2\pi \int\limits_(1)^(2) x(2-x) dx = (4\pi)/(3) = 4.188 }`

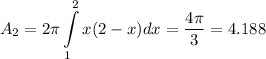
And the sum would be 2.51+4.188 = 6.698

If you revolve just the outer curve you get

If you rotate the first region around the x axis you get that

`{\displaystyle A_1 =\pi \int\limits_(0)^(1) ( √(x))^2 dx = (\pi)/(2) = 1.5708 }`

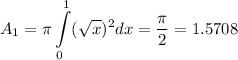
And if you rotate the second region around the x axis you get that

`{\displaystyle A_2 = \pi \int\limits_(1)^(2) (2-x)^2 dx = (\pi)/(3) = 1.0472 }`

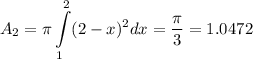
And the sum would be 1.5708+1.0472 = 2.618