Answer:
The general relation about a geoemtric sequence is
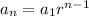
For the first sequence, we have
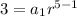
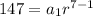
Which is a system of equations. We can isolate a variable in the first equation to replace that expression into the second equation.
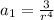
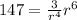
![r^(2)=(147)/(3)\\ r=\sqrt[2]{49}\\r=7](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nfl4t4k0q6nvgzhjyuqyt2fqncuvqnhkq8.png)
Now, we replace this value to find the other one
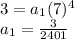
Therefore, the explicit rule function is
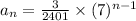
Now, we use the same process for the second sequence.

The second equation is
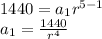
Now, we solve the following expression
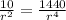
We solve for


Then
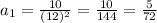
Therefore, the function that models the second sequence is
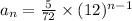
Notice that
 is the dependent variable and
is the dependent variable and
 is the independent variable.
is the independent variable.