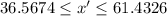Question

The marketing director of a large department store wants to estimate the average number of customers who enter the store every five minutes. She randomly selects five-minute intervals and counts the number of arrivals at the store. She obtains the figures 53, 32, 41, 44, 56, 80, 49, 29, 32, and 74. The analyst assumes the number of arrivals is normally distributed. Using these data, the analyst computes a 95% confidence interval to estimate the mean value for all five-minute intervals. What interval values does she get?

Answer 1

`36.5674\leq x'\leq61.4326`

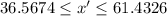
Explanation:

If we assume that the number of arrivals is normally distributed and we don't know the population standard deviation, we can calculated a 95% confidence interval to estimate the mean value as:

`x-t_(\alpha /2)(s)/(√(n) ) \leq x'\leq x-t_(\alpha /2)(s)/(√(n) )`

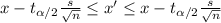
where x' is the population mean value, x is the sample mean value, s is the sample standard deviation, n is the size of the sample,
`\alpha` is equal to 0.05 (it is calculated as: 1 - 0.95) and
`t_(\alpha /2)` is the t value with n-1 degrees of freedom that let a probability of
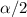`\alpha/2` on the right tail.

So, replacing the mean of the sample by 49, the standard deviation of the sample by 17.38, n by 10 and
`t_(\alpha /2)` by 2.2621 we get:

`49-2.2621(17.38)/(√(10) ) \leq x'\leq 49+2.2621(17.38)/(√(10) )\\49-12.4326\leq x'\leq 49+12.4326\\36.5674\leq x'\leq61.4326`

Finally, the interval values that she get is:

`36.5674\leq x'\leq61.4326`