Question

In a study to estimate the proportion of residents in a city and its suburbs who favor the construction of a nuclear power plant, it was found that 63 of 100 urban residents favor the construction, while only 59 of 125 suburban residents are in favor. If a 95% confidence interval was to be constructed for the difference of the proportions of urban and suburban residents who favor the construction of the plant, what would be the margin of error? Group of answer choices ± 0.0651 ± 0.1289 ± 0.0907 ± 0.1310

Answer 1

`z_(\alpha/2)=1.96`

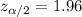
And the margin of error would be:

`ME = 1.96 \sqrt{(0.63*(1-0.63))/(100) +(0.472*(1-0.472))/(125)}= 0.1289`

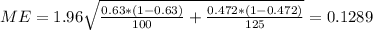
And the best option would be:

± 0.1289

Explanation:

We have the following info given from the problem

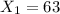`X_1 =63` represent the number urban residents in favor the construction

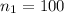`n_1 =100` represent the sample of urban residents

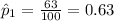`\hat p_1= (63)/(100)=0.63` estimated proportion of urban residents in favor the construction

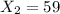`X_2 =59` represent the number suburban residents in favor the construction

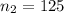`n_2 =125` represent the sample of surban residents

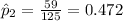`\hat p_2= (59)/(125)=0.472` estimated proportion of suburban residents in favor the construction

And for this case the confidence interval for the difference in the two proportions is given by:

`(\hat p_1 -\hat p_2) \pm z_(\alpha/2) \sqrt{(\hat p_1 (1-\hat p_1))/(n_1) +(\hat p_2 (1-\hat p_2))/(n_2)}`

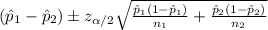
Since the confidence is 95% then the significance level is 5% and the critical value for this case using the normal standard distribution or excel is:

`z_(\alpha/2)=1.96`

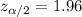
And the margin of error would be:

`ME = 1.96 \sqrt{(0.63*(1-0.63))/(100) +(0.472*(1-0.472))/(125)}= 0.1289`

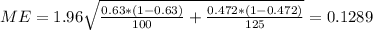
And the best option would be:

± 0.1289