Question

Two loudspeakers in a plane, 5.0 m apart, are playing the same frequency. If you stand 12.0 m in front of the plane of the speak- ers, centered between them, you hear a sound of maximum in- tensity. As you walk parallel to the plane of the speakers, staying 12.0 m in front of them, you first hear a minimum of sound inten- sity when you are directly in front of one of the speakers. What is the frequency of the sound? Assume a sound speed of 340 m/s

Answer 1

The frequency of the sound is 170 Hz

Step-by-step explanation:

Traveling wave is given as;

`D(r,t) = D_o(r)sin(kr- \omega t + \phi_o)`

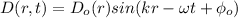
where;

r is the distance from the source

`(kr- \omega t + \phi_o)` is phase

Then phase difference is given as;

`\delta \phi = 2 \pi(\delta r)/(\lambda) +\delta \phi_o`

The phase difference between the two speakers at maximum intensity;

`\delta \phi = 2\pi (\delta r)/(\lambda)`

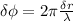
where;

λ is the wavelength

Δr is difference in distance between the two speakers

Δr = r₂ - r₁ =
`√(L^2 + d^2) -L`

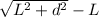
Given;

distance between the two speakers, d = 5.0 m

distance to the plane of the speakers, L = 12.0 m

Δr =
`√(12^2 + 5^2) -12 = 1 \ m`

`\delta \phi = 2\pi(\delta r)/(\lambda)`

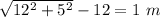
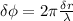
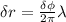`\delta r = (\delta \phi)/(2\pi)\lambda`, at minimum sound intensity, ΔФ = π

`\delta r = (\pi)/(2\pi) \lambda\\\\\delta r = (\lambda)/(2)`

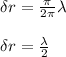
λ = 2Δr

λ = 2 (1) = 2m

`f = (v)/(\lambda) = (340)/(2) = 170\ Hz`

Therefore, the frequency of the sound is 170 Hz

Answer 2

170 Hz

Step-by-step explanation:

The path difference between two waves are given by:

Δ=
`√(12^2 +5^2 )` - 12

Δ = 1 m

In order to hear minimum intensity, the path difference will be

Δ = λ/2

λ = 2Δ

Also, We know that

V= f λ

λ=V/f

Therefore,

340/f = 2 x 1

f= 170 Hz

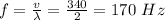
Thus, the frequency of the sound is 170 Hz