Question

A radio talk show host with a large audience is interested in the proportion p of adults in his listening area who think the drinking age should be lowered to eighteen. To find this out, he poses the following question to his listeners: "Do you think that the drinking age should be reduced to eighteen in light of the fact that eighteen-year-olds are eligible for military service?" He asks listeners to phone in and vote "yes" if they agree the drinking age should be lowered and "no" if not. Of the 100 people who phoned in, 70 answered "yes." The margin of error for a 90% confidence interval is:a) 0.045. b) 0.074. c) 0.089. d) 0.690.

Answer 1

The margin of error for a 90% confidence interval is 0.075.

Explanation:

We are given that he asks listeners to phone in and vote "yes" if they agree the drinking age should be lowered and "no" if not.

Of the 100 people who phoned in, 70 answered "yes."

Let
`\hat p` = sample proportion of people who say yes

So,
`\hat p=(X)/(n)` =
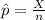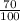`(70)/(100)` = 0.70

where, X = Number of people who say yes = 70

n = Number of people phoned in = 100

Now, Margin of error formula for any confidence interval is given by;

Margin of error =
`Z_(_(\alpha)/(2)_ ) * \text{Standard of Error}`

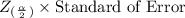
where,
`\alpha` = level of significance = 10%

Standard of error =
`\sqrt{(\hat p(1-\hat p))/(n) }`

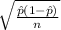
Also, the critical value of x at 5% (
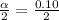`(\alpha)/(2) =(0.10)/(2)`) level of significance is 1.645.

SO, Margin of Error =
`1.645 * \sqrt{(\hat p(1-\hat p))/(n) }`

=
`1.645 * \sqrt{(0.70(1-0.70))/(100) }`

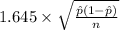
= 0.075

Hence, the margin of error for a 90% confidence interval is 0.075.