Question

According to an​ airline, flights on a certain route are on time 90 90​% of the time. Suppose 20 20 flights are randomly selected and the number of on time flights is recorded. Use technology to find the probabilities. ​(a) Determine whether this is a binomial experiment. ​(b) Find and interpret the probability that exactly 18 18 flights are on time. ​(c) Find and interpret the probability that at least 18 18 flights are on time. ​(d) Find and interpret the probability that fewer than 18 18 flights are on time. ​(e) Find and interpret the probability that between 17 17 and 19 19 ​flights, inclusive, are on time.

Answer 1

(a) Yes, the above experiment is a binomial distribution.

(b) Probability that exactly 18 flights are on time is 28.5%.

(c) Probability that at least 18 flights are on time is 67.7%.

(d) Probability that fewer than 18 flights are on time is 32.3%.

(e) Probability that between 17 and 19 ​flights, inclusive, are on time is 74.5%.

Explanation:

We are given that according to an​ airline, flights on a certain route are on time 90​% of the time.

Suppose 20 20 flights are randomly selected and the number of on time flights is recorded.

The above situation can be represented through binomial distribution;

`P(X = r) = \binom{n}{r} * p^(r) * (1-p)^(n-r);x=0,1,2,3,.......`

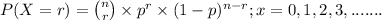
where, n = number trials (samples) taken = 20 flights

r = number of success

p = probability of success which in our question is probability that

flights on a certain route are on time, i.e; p = 0.90

Let X = Number of flights on a certain route that are on time

So, X ~ Binom(n = 20, p = 0.90)

(a) Yes, the above experiment is a binomial distribution as the probability of success is the probability in a single trial.

And also, each flight is independent of another.

(b) Probability that exactly 18 flights are on time is given by = P(X = 18)

P(X = 18) =
`\binom{20}{18} * 0.90^(18) * (1-0.90)^(20-18)`

=
`190 * 0.90^(18) * 0.10^(2)`

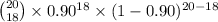
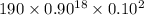
= 0.285

Therefore, probability that exactly 18 flights are on time is 28.5%.

(c) Probability that at least 18 flights are on time is given by = P(X
`\geq` 18)

P(X
`\geq` 18) = P(X = 18) + P(X = 19) + P(X = 20)

=
`\binom{20}{18} * 0.90^(18) * (1-0.90)^(20-18)+\binom{20}{19} * 0.90^(19) * (1-0.90)^(20-19)+\binom{20}{20} * 0.90^(20) * (1-0.90)^(20-20)`

=
`190 * 0.90^(18) * 0.10^(2)+20 * 0.90^(19) * 0.10^(1)+1 * 0.90^(20) * 0.10^(0)`

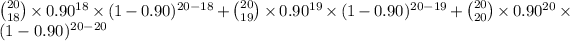
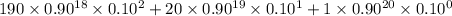
= 0.677

Therefore, probability that at least 18 flights are on time is 67.7%.

(d) Probability that fewer than 18 flights are on time is given by = P(X<18)

P(X < 18) = 1 - P(X
`\geq` 18)

= 1 - 0.677 = 0.323

Therefore, probability that fewer than 18 flights are on time is 32.3%.

(e) Probability that between 17 and 19 ​flights, inclusive, are on time is given by = P(17
`\leq` X
`\leq` 19)

P(17
`\leq` X
`\leq` 19) = P(X = 17) + P(X = 18) + P(X = 19)

=
`\binom{20}{17} * 0.90^(17) * (1-0.90)^(20-17)+\binom{20}{18} * 0.90^(18) * (1-0.90)^(20-18)+\binom{20}{19} * 0.90^(19) * (1-0.90)^(20-19)`

=
`1140 * 0.90^(17) * 0.10^(3)+190 * 0.90^(18) * 0.10^(2)+20 * 0.90^(19) * 0.10^(1)`

= 0.745

Therefore, probability that between 17 and 19 ​flights, inclusive, are on time is 74.5%.