Answer:
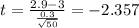
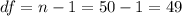
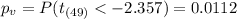
Since the p value is less than the significance level of 0.1 we have enough evidence to reject the null hypothesis and we can conclude that the true growth rate is significantly less than 3 cm per week
Explanation:
Information given
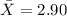 represent the sample mean for the growth
represent the sample mean for the growth
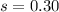 represent the sample standard deviation
represent the sample standard deviation
 sample size
sample size
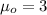 represent the value to check
represent the value to check
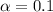 represent the significance level
represent the significance level
t would represent the statistic
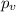 represent the p value for the test
represent the p value for the test
System of hypothesis
We want to verify if the true mean for the growth us less than 3cm per week, the system of hypothesis are:
Null hypothesis:
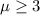
Alternative hypothesis:
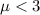
We don't know the population deviation so we can use the t statistic:
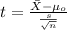 (1)
(1)
Replacing the info given we got:
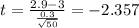
The degrees of freedom are given by:
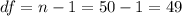
The p value for this case would be given by:
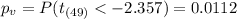
Since the p value is less than the significance level of 0.1 we have enough evidence to reject the null hypothesis and we can conclude that the true growth rate is significantly less than 3 cm per week