Question

A company produces batteries. On average,85% of all batteries produced are good. Each battery is tested before being dispatched, and the inspector correctly classifies the battery 90% of the time. A.What percentage of the batteries will be“classified as good”?B.What is the probability that a battery is defective given that it was classified as good?

Answer 1

a) 78% of the batteries will be classified as good.

b) 1.92% probability that a battery is defective given that it was classified as good

Explanation:

A brief introduction about the conditional probability formula.

Conditional probability formula:

`P(B|A) = (P(A \cap B))/(P(A))`

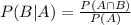
In which

P(B|A) is the probability of event B happening, given that A happened.

Then:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.015)/(0.78) = 0.0192`

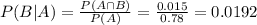
1.92% probability that a battery is defective given that it was classified as good