Answer:
We conclude that college students vote at a lower rate than college faculty which means researcher’s claim was correct.
Explanation:
We are given that a researcher believes that college students vote at a lower rate than college faculty.
She collects data from 200 college faculty and 200 college students using simple random sampling. If 138 of the students and 167 of the faculty voted in the 2008 Presidential election
Let
 = proportion of college students who voted in the 2008 Presidential election.
= proportion of college students who voted in the 2008 Presidential election.
 = proportion of college faculty who voted in the 2008 Presidential election.
= proportion of college faculty who voted in the 2008 Presidential election.
So, Null Hypothesis,
 :
:
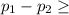 0 or
0 or
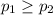 {means that college students vote at a equal or higher rate than college faculty}
{means that college students vote at a equal or higher rate than college faculty}
Alternate Hypothesis,
 :
:
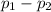 < 0 or
< 0 or
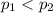 {means that college students vote at a lower rate than college faculty}
{means that college students vote at a lower rate than college faculty}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
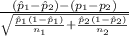 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of college students who voted in the 2008 Presidential election =
= sample proportion of college students who voted in the 2008 Presidential election =
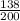 = 0.69
= 0.69
 = sample proportion of college faculty who voted in the 2008 Presidential election =
= sample proportion of college faculty who voted in the 2008 Presidential election =
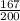 = 0.835
= 0.835
 = sample of college students = 200
= sample of college students = 200
 = sample of college faculty = 200
= sample of college faculty = 200
So, test statistics =

= -3.458
The value of z test statistics is -3.458.
Now, at 5% significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.
Since our test statistics doesn't lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.
Therefore, we conclude that college students vote at a lower rate than college faculty which means researcher’s claim was correct.