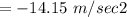Answer:
The description for the given question is described in the explanation section below.
Step-by-step explanation:
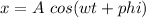 ...(equation 1)
...(equation 1)
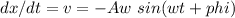 ...(equation 2)
...(equation 2)
at t = 0,
x = 10 &,
v = 0,
From equation 1, we get
⇒
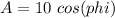 ...(equation 3)
...(equation 3)
⇒
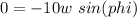
⇒
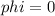
By using this value in equation 3, we get
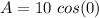
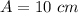
Now from equation 2, we get
 ...(equation 4)
...(equation 4)
As we know,
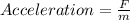
at t = 0,
a = -kA/m
= w2 A
w = root(k/m)
= 15 rad/sec
(b)...
From equation 2, we get
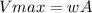
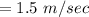
(c)...
From equation 4, we get