Question

Use the quadratic formula to find the roots of y = x2 + 5x + 6:

x = 2 and x = 3
x = 2 and x = -3
x = -2 and x = 3
x = -2 and x = -3
*must show work to receive credit*

Answer 1

x = -2 and x = -3

Explanation:

It is required to find the roots of the equation. The general quadratic equation is :

`ax^2+bx+c=0`

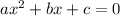
The solution of above equation is:

`x=(-b\pm √(b^2-4ac) )/(2a)`

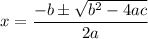
The given equation is :

`x^2+5x+6=0`

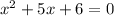
Its solutions are :

`x=(-b+ √(b^2-4ac) )/(2a),(-b- √(b^2-4ac) )/(2a)`

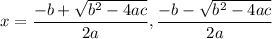
Here, a = 1, b = 5 and c = 6

`x=(-5+ √((5)^2-4* 1* 6) )/(2* 1),(-5- √((5)^2-4* 1* 6) )/(2* 1)\\\\x=-2,-3`

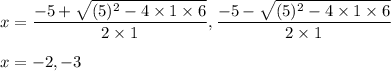
So, the values of x are -2 and -3. Hence, the correct option is (d).