Question

Two parallel surfaces move in opposite directions relative to each other at a velocity of 64 in/sec and are separated by a gap of 0.41 in. The gap is filled by a fluid of unknown viscosity. The relative motion is resisted by a shear stress of 0.42 lb/in2 due to the viscosity of the fluid. If the velocity gradient in the space between the surfaces is constant, determine the viscosity of the fluid in lb·s/in2.

Answer 1

`\mu` = 2.6906 ×
`10^(-3)` lb-s/in²

Step-by-step explanation:

given data

velocity V = 64 in/sec

separated by a gap x = 0.41 in

relative motion by shear stress
`\tau` = 0.42 lb/in²

solution

we know that shear stress is directly proportional to rate of change of velocity as per newton's law of viscosity.

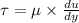`\tau = \mu * (du)/(dy)` ....................1

so here
`\mu` coefficient of dynamic viscosity and
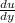`(du)/(dy)` is velocity gradient

and

`\tau = \mu * (v1 - v2 )/(h2-h0)`

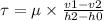
put here value and we get

0.42 =
`\mu * (64)/(0.41)`

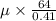
`\mu` = 2.6906 ×
`10^(-3)` lb-s/in²