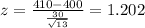Answer:
The idea is test if the true mean operating time without recharging is more than 400 minutes (alternative hypothesis) and the complement would represent the null hypothesis, the system of hypothesis are then:
Null hypothesis:
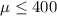
Alternative hypothesis:

Explanation:
Information given
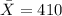 represent the sample mean time of continuous usage without recharging
represent the sample mean time of continuous usage without recharging
 represent the population standard deviation
represent the population standard deviation
 sample size
sample size
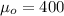 represent the value to check
represent the value to check
 represent the significance level
represent the significance level
t would represent the statistic for the test
 represent the p value for the test
represent the p value for the test
Hypothesis to verify
The idea is test if the true mean operating time without recharging is more than 400 minutes (alternative hypothesis) and the complement would represent the null hypothesis, the system of hypothesis are then:
Null hypothesis:
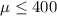
Alternative hypothesis:

Since we don't know the population deviation we need to use the t test with the following statistic:
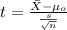 (1)
(1)
Replacing the info we got: