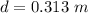Complete Question
The diagram of this question is shown on the first uploaded image
Answer:
The distance the block slides before stopping is
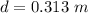
Step-by-step explanation:
The free body diagram for the diagram in the question is shown
From the diagram the angle is

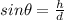
Where
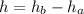
So
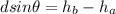
From the question we are told that
The mass of the block is
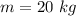
The mass of the pendulum is
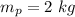
The velocity of the pendulum at the bottom of swing is

The coefficient of restitution is
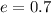
The coefficient of kinetic friction is
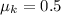
The velocity of the block after the impact is mathematically represented as
![v_2 f = (m_b - em_p)/(m_b + m_p) * v_2 i + ([1 + e] m_1)/(m_1 + m_2 ) v_p](https://img.qammunity.org/2021/formulas/physics/college/wc3a9zjwzmyfi15p8auoeasddta7t6bwh1.png)
Where
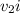 is the velocity of the block before collision which is 0
is the velocity of the block before collision which is 0
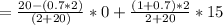
Substituting value
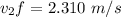
According to conservation of energy principle
The energy at point a = energy at point b
So
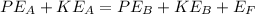
Where
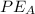 is the potential energy at A which is mathematically represented as
is the potential energy at A which is mathematically represented as
 = 0 at the bottom
= 0 at the bottom
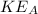 is the kinetic energy at A which is mathematically represented as
is the kinetic energy at A which is mathematically represented as
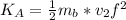
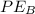 is the potential energy at B which is mathematically represented as
is the potential energy at B which is mathematically represented as
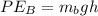
From the diagram
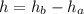
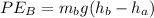
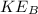 is the kinetic energy at B which is 0 (at the top )
is the kinetic energy at B which is 0 (at the top )
Where is
 is the workdone against velocity which from the diagram is
is the workdone against velocity which from the diagram is
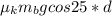
So
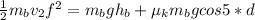
Substituting values

So