Answer:
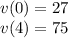
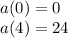
Explanation:
The function of the distance is equal to:
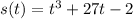
If we have the distance function, the velocity function is the derivative of s(t). So, the velocity function v(t) is equal to:
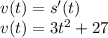
Then, the velocity at t=0 and t=4 are calculated as:
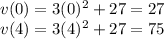
So, the velocity at 0 seconds is equal to 27 cm/sec and the velocity at 4 seconds is equal to 75 cm/sec
At the same way, the acceleration function is the derivative of the velocity function. So, the acceleration function a(t) is equal to:
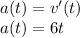
Then, the acceleration at t=0 and t=4 is:
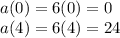
Therefore, the acceleration at 0 seconds is equal to 0
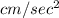 and the acceleration at 4 seconds is equal to 24
and the acceleration at 4 seconds is equal to 24
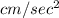 .
.