Answer:
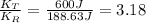
Step-by-step explanation:
To find the rotational kinetic energy you first calculate the angular acceleration by using the following formula:
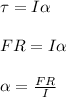
F: force applied
R: radius of the wheel
I: moment of inertia
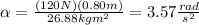
With this value you calculate the angular velocity:
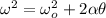
you calculate how many radians the wheel run in 5.0m
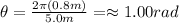
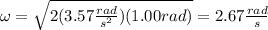
Next, you use the formula for the rotational kinetic energy:
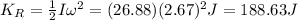
For the transnational kinetic energy you use the following equation:
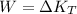 (net work equals the change in the kinetic energy).
(net work equals the change in the kinetic energy).
By replacing the you obtain:
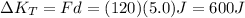
Finally, the ratio between translational rotational kinetic energy is:
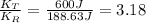
hence, translational kinetic energy is three times the rotational kinetic energy.