Question

Convert the equation r cosine theta equals 9 sine (2 theta )to Cartesian coordinates. Describe the resulting curves. Choose the correct equations below. A. (x minus 9 )squared plus y squared equals 9 squared and x equals 0 B. x squared plus y squared equals 9 squared and x equals 0 C. x squared plus (y minus 9 )squared equals 9 squared and x equals 0 Your answer is correct.D. (x minus 9 )squared plus (y minus 9 )squared equals 9 squared and x equals 0 Choose the best description of the curves described by this equation. A. a circle centered at (negative 9 comma 0 )with a radius of 9 and the y dash axis B. a circle centered at (0 comma 9 )with a radius of 9 and the y dash axis Your answer is correct.C. a circle centered at (0 comma negative 9 )with a radius of 9 and the y dash axis D. a circle centered at (9 comma 0 )with a radius of 9 and the y dash axis

Answer 1

The curve is a circle of radius 9 centered at the point (0,9) and the equation is
`x^2+(y-9)^2 = 81`

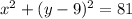
Explanation:

Proceed as follows:

`r\cos(\theta) = 9 \sin(2\theta)`

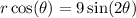
Take
`\sin(2\theta) = 2\sin(\theta)\cos(\theta)`. Then

`r\cos(\theta) = 9 \sin(2\theta)= 18 \sin(\theta) \cos(\theta)`

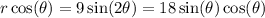
Multiply both side by
`r^2`. Then

`r^2\cdot r\cos(\theta) = 18 \cdot r\sin(\theta) \cdot r\cos(\theta)`

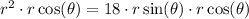
Use the following substitution
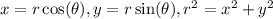`x = r\cos(\theta), y = r\sin(\theta), r^2 = x^2+y^2`. Then

`(x^2+y^2)\cdot (x) = 18 \cdot (x)\cdot(y)`

By cancelling out x on both sides we get the following equation

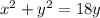`x^2+y^2 = 18y` or
`x^2+y^2-18y =0`

Recall that given a expression of the form
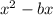`x^2-bx` we can complete the square by adding an substracting the amount
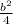`(b^2)/(4)`. So, we get
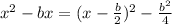`x^2-bx = (x-(b)/(2))^2-(b^2)/(4)`. In our case, we will complete the square for y, then

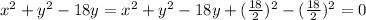`x^2+y^2-18y = x^2+y^2-18y+((18)/(2))^2-((18)/(2))^2 = 0`. Then

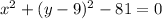`x^2+(y-9)^2-81=0` or

`x^2+(y-9)^2 = 81`.

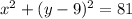Recall that the equation of a circle is given by
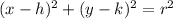`(x-h)^2+(y-k)^2 = r^2` where (h,k) is the center of the circle and r is the radius. In our case we have h=0, k = 9 and r = 9. So it is a circle of radius 9 centered at the point (0,9)