Answer:
see below
Explanation:
cscx=4
sinx=1/4
cosx=-√(1-sin^2x)=-√(1-(1/16))=-√(15/16)=-√15/4
note: cos<0,sin>0 in quadrant II
sin(x/2)=
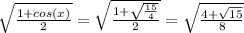
cos(x/2)=
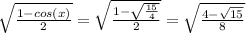
tan(x/2)=
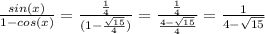
Calculator check:
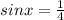
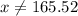 ˚ in quadrant II
˚ in quadrant II
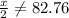 ˚
˚
sin(x/2)≈sin(82.76)≈0.9920..
exact value=√(4+√15)/8≈0.9920..
..
cos(x/2)≈cos(82.76)≈0.1260..
exact value=√(4-√15)/8≈0.1260..
..
tan(x/2)=tan(82.76)≈7.872..
exact value=1/(4-√15)≈7.872..