Question

Personnel tests are designed to test a job​ applicant's cognitive​ and/or physical abilities. A particular dexterity test is administered nationwide by a private testing service. It is known that for all tests administered last​ year, the distribution of scores was approximately normal with mean 72 and standard deviation 8.1. a. A particular employer requires job candidates to score at least 78 on the dexterity test. Approximately what percentage of the test scores during the past year exceeded 78​? b. The testing service reported to a particular employer that one of its job​ candidate's scores fell at the 95th percentile of the distribution​ (i.e., approximately 95​% of the scores were lower than the​ candidate's, and only 5​% were​ higher). What was the​ candidate's score?

Answer 1

(a) 22.96% of the test scores during the past year exceeded 78.

(b) The​ candidate's score was 85.32.

Explanation:

We are given that a particular dexterity test is administered nationwide by a private testing service.

It is known that for all tests administered last​ year, the distribution of scores was approximately normal with mean 72 and standard deviation 8.1.

Let X = distribution of test scores

SO, X ~ Normal(
`\mu=72, \sigma^(2) =8.1^(2)`)

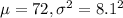The z score probability distribution for normal distribution is given by;

Z =
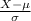`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean score = 72

`\sigma` = standard deviation = 8.1

(a) Now, percentage of the test scores during the past year which exceeded 78​ is given by = P(X > 78)

P(X > 78) = P(
`(X-\mu)/(\sigma)` >
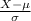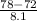`(78-72)/(8.1)` ) = P(Z > 0.74) = 1 - P(Z < 0.74)

= 1 - 0.7704 = 0.2296

The above probability is calculated by looking at the value of x = 0.74 in the z table which has an area of 0.77035.

Therefore, 22.96% of the test scores during the past year exceeded 78.

(b) Now, we given that the testing service reported to a particular employer that one of its job​ candidate's scores fell at the 95th percentile of the distribution and we have to find the candidate's score, that means;

P(X > x) = 0.05 {where x is the required candidate score}

P(
`(X-\mu)/(\sigma)` >
`(x-72)/(8.1)` ) = 0.05

P(Z >
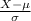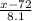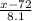`(x-72)/(8.1)` ) = 0.05

Now, in the z table the critical value of x which represents the top 5% area is given as 1.645, i.e;

`(x-72)/(8.1) = 1.645`

`{x-72} = 1.645 * 8.1`

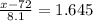
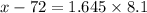
x = 72 + 13.32 = 85.32

Hence, the​ candidate's score was 85.32.