Question

A study of 4,430 U.S. adults found that 2,913 were obese or overweight. The 95% confidence interval for the proportion of adults in U.S. who are obese or overweight is

Answer 1

Answer: (0.644,0.672)

Explanation:

Let p be the proportion of the adults in U.S. who are obese or overweight.

Confidence interval for p will be :

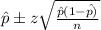`\hat{p}\pm z\sqrt{\frac{\hat{p}(1-\hat{p)}}{n}}`, where
`\hat{p}` is sample proportion , n is sample size , and z is the critical z value as per confidence level.

As per given, we have

n= 4430

`\hat{p}=(2913)/(4430)\approx0.658`

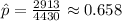
Critical z-value for 95% confidence level is 1.96.

Then, the 95% confidence interval for the proportion of adults in U.S. who are obese or overweight would be:

`0.658\pm (1.96)\sqrt{(0.658(1-0.658))/(4430)}\\\\=0.658\pm1.96*0.0071272851865\\\\=0.658\pm0.0139694789655\\\\\approx(0.658-0.014,0.658+0.014)\\\\=(0.644,0.672)`

Hence, the required 95% confidence interval would be (0.644,0.672).