Question

When Harper commutes to work, the amount of time it takes her to arrive is normally distributed with a mean of 24 minutes and a standard deviation of 3 minutes. Using the empirical rule, determine the interval that represents the middle 95% of her commute times.

Answer 1

`\mu -2\sigma = 24-2*3= 18`

`\mu -2\sigma = 24+2*3= 30`

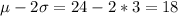
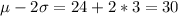
So then we can conclude that we expect the middle 95% of the values within 18 and 30 minutes for this case

Explanation:

For this case we can define the random variable X as the amount of time it takes her to arrive to work and we know that the distribution for X is given by:

`X \sim N(\mu = 24, \sigma =3)`

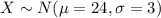
And we want to use the empirical rule to estimate the middle 95% of her commute times. And the empirical rule states that we have 68% of the values within one deviation from the mean, 95% of the values within two deviations from the mean and 99.7 % of the values within 3 deviations from the mean. And we can find the limits on this way:

`\mu -2\sigma = 24-2*3= 18`

`\mu -2\sigma = 24+2*3= 30`

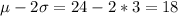
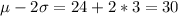
So then we can conclude that we expect the middle 95% of the values within 18 and 30 minutes for this case