Question

A study was conducted to estimate the difference in the mean salaries of elementary school teachers from two neighboring states. A sample of 10 teachers from the Indiana had a mean salary of $28,900 with a standard deviation of $2300. A sample of 14 teachers from Michigan had a mean salary of $30,300 with a standard deviation of $2100. Determine a 95% confidence interval for the difference between the mean salary in Indiana and Michigan.(Assume population variances are different.)

Answer 1

`(28900-30300) -2.07 \sqrt{(2300^2)/(10) +(2100^2)/(14)} = -3301.70`

`(28900-30300) +2.07 \sqrt{(2300^2)/(10) +(2100^2)/(14)} = 501.698`

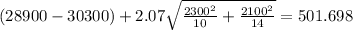
The confidence interval would be
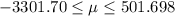`-3301.70 \leq \mu \leq 501.698` and since the confidence interval contains the value of 0 we don't have enough evidence to conclude that the difference between the two states for the salary of teachers are significantly different.

Explanation:

We have the following info given by the problem

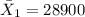`\bar X_1 = 28900` the sample mean for the salaries of teachers in Indiana

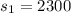`s_1 = 2300` the sample deviation for the salary of teachers in Indiana

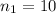`n_1 =10` the sample size from Indiana

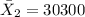`\bar X_2 = 30300` the sample mean for the salaries of teachers in Michigan

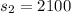`s_2 = 2100` the sample deviation for the salary of teachers in Michigan

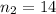`n_2 =14` the sample size from Michigan

We want to find a confidence interval for the difference in the two means and the formula for this case is given by;

`(\bar X_1 -\bar X_2) \pm t_(\alpha/2)\sqrt{(s^2_1)/(n_1) +(s^2_2)/(n_2)}`

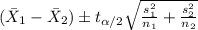
The degrees of freedom for this case are:

`df = n_1 +n_2 -2= 10+14-2 =22`

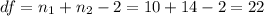
The confidence is 95%so then the significance is
`\alpha=0.05` and the
`\alpha/2 =0.025`, we need to find a critical value in the t distribution with 22 degrees of freedom who accumulates 0.025 of the area on each tail and we got:

`t_(\alpha/2)= 2.07`

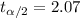
And now replacing in the formula for the confidence interval we got:

`(28900-30300) -2.07 \sqrt{(2300^2)/(10) +(2100^2)/(14)} = -3301.70`

`(28900-30300) +2.07 \sqrt{(2300^2)/(10) +(2100^2)/(14)} = 501.698`

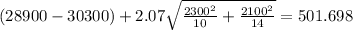
The confidence interval would be
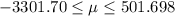`-3301.70 \leq \mu \leq 501.698` and since the confidence interval contains the value of 0 we don't have enough evidence to conclude that the difference between the two states for the salary of teachers are significantly different.