Question

What is the length of the diagonal, d, of the rectangular prism shown below?

Round your answer to the nearest tenth.​

Answer 1

The diagonal of the volumetric figure is 7 units long.

Explanation:

The figure is attached.

Notice that the dimensions of the prism are

`w=2\\l=3\\h=6`

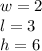
First, we need to find the diagonal of the rectangular face on the base, this diagonal of the base is part of the right triangle formed by the diagonal of the volume, that's why we need it.

Let's use the Pythagorean's Theorem

`d_(base)=\sqrt{2^(2) +3^(2) }=√(4+9)=√(13)`

This diagonal of the base is a leg in the right triangle formed by the diagonal of the volume.

Let's use again Pythagorean's Theorem

`d_(volume)=\sqrt{(√(13) )^(2) +(6)^(2) } =√(13+36)=√(49)\\ d_(volume)=7 \ units`

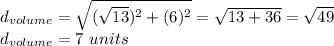
Therefore, the diagonal of the volumetric figure is 7 units long.