Answer:
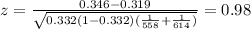
Now we can calculate the p value with this probability:
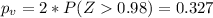
Since the p value is higher than the significance level we have enough evidence to FAIL to reject the null hypothesis and we don't have enough evidence to conclude that the two recognition rates are different
Explanation:
Information given
 represent the number of people who knew the product in New York
represent the number of people who knew the product in New York
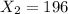 represent the number of people who knew the product in California
represent the number of people who knew the product in California
 sample 1 from New York
sample 1 from New York
 sample 2 from California
sample 2 from California
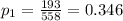 represent the proportion of people who knew the product in New York
represent the proportion of people who knew the product in New York
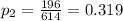 represent the proportion of people who knew the product in California
represent the proportion of people who knew the product in California
 represent the pooled estimate of p
represent the pooled estimate of p
z would represent the statistic
 represent the value for the test
represent the value for the test
 significance level
significance level
System of hypothesis
We want to verify if the recognition rates are the same in both states, the system of hypothesis are:
Null hypothesis:
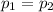
Alternative hypothesis:
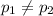
The statistic for this case is given by:
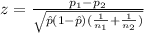 (1)
(1)
Where
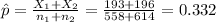
The statistic for this case is given by:
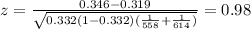
Now we can calculate the p value with this probability:
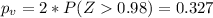
Since the p value is higher than the significance level we have enough evidence to FAIL to reject the null hypothesis and we don't have enough evidence to conclude that the two recognition rates are different