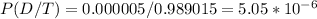Question

A screening test for a certain disease is used in a large population of people of whom 1 in 1000 actually have the disease. Suppose that the false positive rate is 1% and the false negative rate is 0.5%. Thus a person who has the disease tests positive for it 99.5% of the time, and a person who does not have the disease tests negative for it 99% of the time. What is the probability that a randomly chosen person who tests negative for the disease actually has the disease

Answer 1

`P(D/T)=5.05*10^(-6)`

Explanation:

Let's call D the event that a person has the disease, D' the event that a person doesn't have the disease and T the event that the person tests negative for the disease.

So, the probability P(D/T) that a randomly chosen person who tests negative for the disease actually has the disease is calculated as:

P(D/T) = P(D∩T)/P(T)

Where P(T) = P(D∩T) + P(D'∩T)

So, the probability P(D∩T) that a person has the disease and the person tests negative for the disease is equal to:

P(D∩T) = (1/1000)*(0.005) = 0.000005

Because 1/1000 is the probability that the person has the disease and 0.005 is the probability that the person tests negative given that the person has the disease.

At the same way, the probability P(D'∩T) that a person doesn't have the disease and the person tests negative for the disease is equal to:

P(D'∩T) = (999/1000)*(0.99) = 0.98901

Finally, P(T) and P(D/T) are equal to:

P(T) = 0.000005 + 0.98901 = 0.989015

`P(D/T) = 0.000005/0.989015 = 5.05*10^(-6)`