Question

If one cylinder is r=3 ft and the volume is 756 feet cubed, how do I find the volume of a larger cylinder with a radius of 7feet?

Answer 1

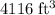`4116\; {\rm ft^(3)}`, assuming that the two cylinders are of the same height.

Explanation:

The volume of a cylinder of radius
`r` and height
`h` is
`\pi\, r^(2)\, h`.

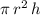If the two cylinders are of the same height
`h`, the volume of the two cylinders would be proportional to the square of their radii.

Let
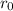`r_(0)` and
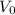`V_(0)` denote the radius and volume of the smaller cylinder. Similarly, let
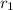`r_(1)` and
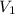`V_(1)` denote the radius and volume of the larger cylinder. Assuming that the height of both cylinders is
`h`:

`V_(1) = \pi\, {r_(1)}^(2)\, h`.

`V_(0) = \pi\, {r_(0)}^(2)\, h`.

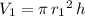Hence,
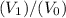`(V_(1)) / (V_(0))` (ratio between the volume of the larger cylinder and the volume of the smaller cylinder) would be:

`\begin{aligned}(V_(1))/(V_(0)) &= \frac{\pi\, {r_(1)}^(2)\, h}{\pi\, {r_(0)}^(2)\, h} =\frac{{r_(1)}^(2)}{{r_(0)}^(2)}\end{aligned}`.

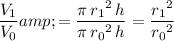In this question, it is given that:

• the volume of the smaller cylinder is
  `V_(0) = 756\; {\rm ft^(3)}`.
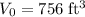• the radius of the smaller cylinder is
  `r_(0) = 3\; {\rm ft}`.
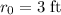• the radius of the larger cylinder is
  `r_(1) = 7\; {\rm ft}`.

Rearrange the equation
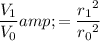`\begin{aligned}(V_(1))/(V_(0)) &= \frac{{r_(1)}^(2)}{{r_(0)}^(2)}\end{aligned}` to find an expression for
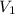`V_(1)`, volume of the larger cylinder:

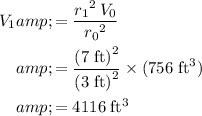`\begin{aligned}V_(1) &= \frac{{r_(1)}^(2)\, V_(0) }{{r_(0)}^(2)} \\ &= \frac{{(7\; {\rm ft})}^(2)}{{(3\; {\rm ft})}^(2)} * (756\; {\rm ft^(3)}) \\ &= 4116\; {\rm ft^(3)} \end{aligned}`.