Question

asked Apr 22, 2021 83 views

1 Answer

Mhartington · Answer 1 · 2021-04-28T20:07:14+0000

Answer:

2.99% probability that the cost will be paid by only one team

Explanation:

The binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)

In which
C_(n,x) is the number of different combinations of x objects from a set of n elements, given by the following formula.

C_(n,x) = (n!)/(x!(n-x)!)

And p is the probability of X happening.

Probability that a team plays:

A team plays if it has at most 2 injured players out of 11.

11 players, so
n = 11

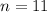
Each player with a 5% probability of injury, so
p = 0.05

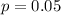
Then

$P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)$

In which

P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)

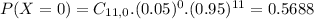
P(X = 0) = C_(11,0).(0.05)^(0).(0.95)^(11) = 0.5688

P(X = 1) = C_(11,1).(0.05)^(1).(0.95)^(10) = 0.3293

P(X = 2) = C_(11,2).(0.05)^(2).(0.95)^(9) = 0.0867

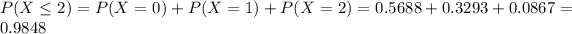
$P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.5688 + 0.3293 + 0.0867 = 0.9848$

Each team has a 0.9848 probability of showing up to play.

What is the probability that the cost will be paid by only one team?

This happens if one team shows up and the other do not.

2 teams, so
n = 2

Each team has a 0.9848 probability of showing up to play, so
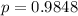p = 0.9848 .

This probability is P(X = 1).

P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)

P(X = 1) = C_(2,1).(0.9848)^(1).(0.0152)^(1) = 0.0299

2.99% probability that the cost will be paid by only one team

Please log in or register to add a comment.