Answer:
.356
Step-by-step explanation:
p = .25, the chance of getting an albino
q = .75, the chance of getting not an albino
n = 6, the number of offspring
r = 1, the number of albinos we want
What's the probability of getting exactly 1 out of six? This is called a binomial distribution. The formula is
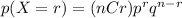
nCr means n choose r, which you can find on your calculator (on a TI-84, it's MATH->PRB->nCr).

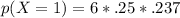
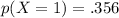
That's a fairly low percentage, which makes sense, because you'd expect 1.5 albinos, if this were a statistically perfect world.