Question

What is the wavelength of a photon with an energy of 4.56 x 10-19 J?

• A. 502 nm
• B. 436 nm
C. 688 nm
D. 460 nm

Answer 1

B

Step-by-step explanation:

We can use Planck's equation. Recall that:

`\displaystyle E = h\\u`

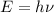
Where h is Planck's constant and ν is the frequency.

We also have that:

`\displaystyle \lambda \\u = c`

Where c is the speed of light and λ is the wavelength. Hence:

`\displaystyle \\u = (c)/(\lambda)`

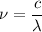
Therefore:

`\displaystyle E= h\left((c)/(\lambda)\right)`

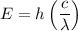
Solving for λ yields:

`\displaystyle \lambda = (hc)/(E)`

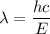
Hence substitute. Recall that h = 6.626 × 10⁻³⁴ Js and c = 2.998 × 10⁸ m/s:

`\displaystyle \begin{aligned} \lambda & = \frac{(6.626* 10^(-34)\text{ Js})(2.998* 10^8\text{ m/s})}{4.56* 10^(-19) \text{ J}} \left(\frac{1* 10^9\text{ nm}}{1\text{ m}}\right) \\ \\ & = 436\text{ nm}\end{aligned}`

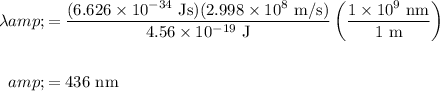
In conclusion, our answer is B.