Question

A farmer has both sheep and chickens on his farm. All the animals have the expected number of parts. When his animals are all

together, there are 90 legs and 32 heads. How many of each animal does he have?

Answer 1

13 sheep, 19 chicken

Explanation:

You can start to solve this problem by assigning variables. First, let's assign the number of sheep there are as
`x` and the number of chickens there are as
`y`.

Because each sheep has 4 legs, the number of legs for each sheep would be
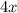`4x`. Similarly, because each chicken has 2 legs, the number of legs for each chicken would be
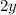`2y`. Each animal would have 1 head, so the number of heads would just be
`x` and
`y`. Because the number of legs in total are 90,
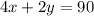`4x + 2y=90`. Because the number of heads in total are 32,
`x+y=32.`

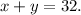
There is now a system of equations with two unknown variables and two equations. There are many ways to solve this, but for me, the easiest would be elimination. First, I would double the second equation,
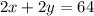`2x+2y=64`. Then, I would subtract that from the first equation, eliminating
`y`.
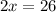`2x=26`. Solving for x gives 13. We can then plug that value into the second equation, making y be
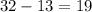`32-13=19`. This means that
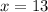`x=13` and
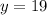`y=19`, meaning that there are 13 sheep and 19 chicken.