2 Answers

Crissal · Answer 1 · 2021-07-17T15:58:36+0000

Answer:

P(x < 92) is 0.16

Explanation:

We are given that the normal distribution has a mean of 98 and a standard deviation of 6.

Mean =
$\mu = 98$

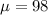
Standard deviation =
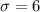
$\sigma = 6$

We are supposed to find P(x < 92)

Formula :
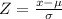
$Z=(x-\mu)/(\sigma)$

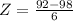
Z=(92-98)/(6)

Z=-1

Refer the z table for p value

So,p value = 0.1587

So, P(x < 92) is 0.16

Option A is true

Hence P(x < 92) is 0.16

Please log in or register to add a comment.