Question

The equation

24x2 + 25x − 47/ax−2 = −8x − 3 − 53/ax−2 is true for all values of x≠2/a, where a is a constant.

What is the value of a?

A) -16
B) -3
C) 3
D) 16

Answer 1

a = -3

Step-by-step explanation:

Using the leading terms of the polynomial and quotient, we can find the leading term of the divisor

24x²/ax = -8x

24x² = -8ax²

-8a = 24

a = 24/-8

a = -3

Answer 2

B. -3

Step-by-step explanation:

Our equation is:
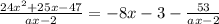`(24x^2+25x-47)/(ax-2) =-8x-3-(53)/(ax-2)` . We see that both sides have a term with denominator ax - 2, so let's add
`(53)/(ax-2)` to both sides:

`(24x^2+25x-47)/(ax-2) =-8x-3-(53)/(ax-2)`

`(24x^2+25x-47)/(ax-2)+(53)/(ax-2) =-8x-3`

`(24x^2+25x+6)/(ax-2)=-8x-3`

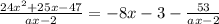
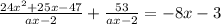
Now multiply both sides by ax - 2:

`24x^2+25x+6=(-8x-3)(ax-2)=-8ax^2-3ax+16x+6`

`24x^2+25x+6=(-8a)x^2+(16-3a)x+6`

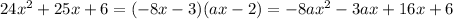
We essentially want to make the terms on each side match. Look at the coefficient of x² on the left side: it's 24. That means on the right side, it should be 24, as well. Then, set -8a equal to 24:

-8a = 24

a = -3

Thus, the answer is B.