We have been given that the lifespans of lions in a particular zoo are normally distributed. The average lion lives 12.5 years; the standard deviation is 2.4 years. We are asked to find the probability of a lion living longer than 10.1 years using empirical rule.
First of all, we will find the z-score corresponding to sample score 10.1.
 , where,
, where,
z = z-score,
x = Random sample score,
 = Mean
= Mean
 = Standard deviation.
= Standard deviation.
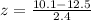
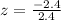

Since z-score of 10.1 is
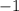 . Now we need to find area under curve that is below one standard deviation from mean.
. Now we need to find area under curve that is below one standard deviation from mean.
We know that approximately 68% of data points lie between one standard deviation from mean.
We also know that 50% of data points are above mean and 50% of data points are below mean.
To find the probability of a data point with z-score
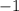 , we will subtract half of 68% from 50%.
, we will subtract half of 68% from 50%.

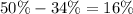
Therefore, the probability of a lion living longer than 10.1 years is approximately 16%.